Triangle de puissance : formule et exemples

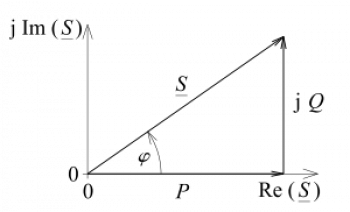
Le triangle de puissance, également connu sous le nom de triangle de Watt, est une représentation graphique utilisée en théorie électrique pour analyser la distribution de puissance dans un circuit à courant alternatif (CA).

Il est basé sur les propriétés trigonométriques d'un triangle rectangle, ce qui nous permet de calculer et de comprendre la relation entre les trois puissances fondamentales d'un système électrique :

1. Puissance apparente ($S$) : Représente la puissance totale fournie au circuit et est mesurée en voltampères (VA). Il s'agit de la combinaison vectorielle de la puissance active et réactive.
2. Puissance active ($P$) : C'est la puissance utile qui est transformée en travail réel, comme l'éclairage ou le mouvement des moteurs. Elle est mesurée en watts (W).
3. Puissance réactive ($Q$) : C'est la puissance qui n'effectue pas de travail utile mais qui est nécessaire au fonctionnement des équipements comportant des éléments inductifs (tels que les transformateurs et les moteurs). Elle est mesurée en volt-ampères réactifs (VAR).

Formule du triangle de puissance

Le triangle est composé de trois côtés, où :

• L'hypoténuse représente la puissance apparente ($S$).
• La branche adjacente est la puissance active ($P$), liée au cosinus de l'angle de phase ($\cos \theta$).
• La branche opposée est la puissance réactive ($Q$), liée au sinus de l'angle de phase ($\sin \theta$).
• Mathématiquement, la relation entre ces puissances est exprimée par le théorème de Pythagore :

$$S^2=P^2+Q^2$$

Le facteur de puissance (PF) est défini comme le rapport entre la puissance active et la puissance apparente :

$$FP=\cos \theta =\frac{P}{S}$$

Lorsque le facteur de puissance est faible, cela signifie qu'il y a une forte proportion de puissance réactive, ce qui réduit l'efficacité du système électrique.

Exemples pratiques du triangle de puissance

Ci-dessous, nous montrons trois exemples pratiques

Moteur électrique à faible facteur de puissance

Un moteur à induction consomme 10 kW de puissance active et a une puissance réactive de 6 kVAR en raison de sa nature inductive.

La puissance apparente sera :

$$S=\sqrt{({10}^2+6^2)}=\sqrt{100+36}=\sqrt{136}\text{environ}11,66\text{ kVA}$$

Système d'éclairage avec correction du facteur de puissance

Un ensemble de lampes LED consomme 5 kW avec une puissance réactive de 1 kVAR.

La puissance apparente sera :

$$S=\sqrt{(5^2+1^2)}=\sqrt{25+1}=\sqrt{26}\text{environ}5,1\text{ kVA}$$

Transformateur avec charge inductive

Un transformateur fournit 50 kW à un système avec une charge inductive nécessitant 30 kVAR.

La puissance apparente du système sera :

$$S=\sqrt{({50}^2+{30}^2)}=\sqrt{2500+900}=\sqrt{3400}\text{environ}58,3\text{ kVA}$$

À quoi sert le triangle de puissance ?

Le triangle de puissance est un outil fondamental dans l’analyse et la conception des systèmes électriques. Ses applications comprennent :

Calcul de la puissance électrique

Il permet de déterminer la répartition de puissance dans un circuit :

• La puissance apparente totale (S) fournie.
• Puissance active (P), qui est convertie en énergie utile.
• Puissance réactive (Q), qui représente l'énergie échangée entre les composants inductifs et capacitifs.

Optimisation des performances du circuit

En comprenant la distribution de puissance, les pertes d’énergie peuvent être minimisées et le facteur de puissance amélioré, réduisant ainsi la consommation inutile de puissance réactive et optimisant l’utilisation du réseau électrique.

Conception de systèmes électriques

Il est utilisé pour dimensionner les équipements électriques, garantissant que les transformateurs, les générateurs et les câbles sont capables de gérer la puissance requise sans surcharge ni pertes excessives.

Correction du facteur de puissance

De nombreux systèmes électriques industriels nécessitent des batteries de condensateurs pour compenser la puissance réactive et améliorer le facteur de puissance, réduisant ainsi la demande énergétique du réseau et diminuant les coûts d'exploitation.

Analyse des pannes et maintenance préventive

Le triangle de puissance permet de détecter les problèmes dans les systèmes électriques, tels que les pertes d'énergie dues à une réactance élevée ou à des déséquilibres de charge, contribuant ainsi à prévenir les pannes et à optimiser la maintenance.

Exercice résolu sur le triangle de puissance

Déclaration:

Il s'agit d'un circuit électrique d'une puissance apparente de 800 VA et d'un facteur de puissance de 0,8. Calculer la puissance active et la puissance réactive du circuit.

Solution:

Tout d'abord, nous pouvons calculer la puissance active (P) du circuit en utilisant la formule P = S x cos(θ), où θ est l'angle de phase entre le courant et la tension. Dans ce cas, puisque le facteur de puissance (PF) est égal à 0,8, nous savons que cos(θ) = PF = 0,8. Nous pouvons donc calculer la puissance active comme suit :

\[
P = 800 \, VA \fois 0,8 = 640 \, W
\]

La puissance active du circuit est de 640 watts.

Ensuite, nous pouvons calculer la puissance réactive (Q) du circuit en utilisant la formule Q = S x sin(θ). Nous savons que l'angle de phase (θ) peut être calculé à partir du facteur de puissance en utilisant la formule suivante :

\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]

Dans ce cas, puisque FP = 0,8, nous pouvons calculer sin(θ) comme suit :

\[
\sin(\theta) = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
\]

Par conséquent, nous pouvons calculer la puissance réactive comme suit :

\[
Q = 800 \, VA \fois 0,6 = 480 \, VAR
\]

La puissance réactive du circuit est de 480 volts-ampères réactifs.

Par conséquent, la puissance active du circuit est de 640 W et la puissance réactive est de 480 VAR.

Auteur: Oriol Planas - Ingénieur Technique Industriel

Date de Publication: 26 avril 2023
Dernière Révision: 27 mars 2025