Le triangle, figure géométrique composée de trois segments qui relient trois sommets différents non alignés, représente l'une des formes polygonales fondamentales en géométrie. Son importance dans la science et la technologie remonte à l’Antiquité, puisqu’il s’agit de l’une des figures géométriques les plus essentielles et les plus utilisées.
Une caractéristique importante des triangles est leur invariabilité, ce qui en fait des éléments cruciaux dans la conception architecturale, comme la Tour Eiffel, basée sur une composition de formes triangulaires, et dans l'ingénierie, y compris les structures fixes pour les panneaux solaires. De plus, ils jouent un rôle fondamental en géométrie, puisque tous les polygones peuvent être décomposés en triangles.
Caractéristiques des triangles
Les triangles sont des figures géométriques fondamentales présentant diverses caractéristiques qui définissent leur structure et leurs propriétés. Voici quelques-unes des caractéristiques les plus importantes des triangles :
- Trois côtés : Les triangles sont des polygones qui ont exactement trois côtés. Ces côtés sont des segments de droite qui relient trois points appelés sommets.
- Trois angles : Chaque triangle est constitué de trois angles intérieurs à ses sommets.
- Somme des angles : Dans un triangle, la somme des angles intérieurs est égale à 180 degrés. Ceci est valable pour tout type de triangle, qu'il soit équilatéral, isocèle ou scalène.
- Côtés et angles correspondants : Dans un triangle, les côtés et angles correspondants sont égaux dans les triangles congrus. La congruence fait référence à l'égalité de forme et de taille.
- Hauteur et médiane : Dans un triangle, la hauteur est un segment de droite perpendiculaire à un côté et passant par le sommet opposé. La médiane est un segment qui relie un sommet au milieu du côté opposé.
Types de triangles
Ces figures géométriques peuvent être classées selon différents critères :
En raison de la taille des angles intérieurs, il peut s'agir de :
- Triangle aigu : tous les angles intérieurs sont aigus (inférieurs à 90 degrés).
- Triangle obtus : il y a un angle supérieur à 90 degrés.
- Triangle rectangle : L'un des angles fait 90 degrés, un angle droit. Dans ce cas, les deux côtés qui forment un angle droit sont appelés jambes et le côté opposé à l’angle droit est appelé hypoténuse.
Comme en géométrie euclidienne, la somme des angles d'un triangle est de 180º. Par conséquent, au moins deux angles du triangle doivent être aigus (moins de 90º).
En raison du nombre de côtés égaux, ces figures peuvent être :
- Triangle scalène : les trois côtés ne sont pas égaux.
- Triangle isocèle s : deux côtés sont égaux. Ces côtés sont appelés côté, le troisième côté est appelé base. Dans un triangle isocèle, les angles à la base sont égaux.
- Triangle équilatéral : les trois côtés sont égaux. Dans un triangle équilatéral, tous les angles sont égaux à 60°.
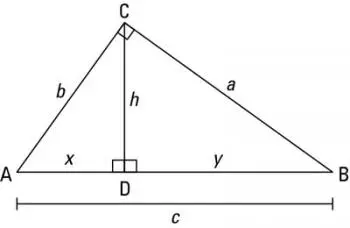
Calculer l'aire et le périmètre d'un triangle
A partir de la figure du bas, pour obtenir le périmètre et l'aire d'un triangle, on peut utiliser les formules suivantes :
Périmètre
Pour calculer le périmètre il faut simplement additionner les longueurs des côtés de la figure : a + b + c.
Zone
La formule pour trouver l'aire d'un triangle est la moitié du produit de la base (pas des côtés) et de la hauteur :
A = (b h) / 2
Dans le cas où on ne connaît pas la hauteur, on peut appliquer la formule de Heron.
Où:
-
a, b et c correspondent aux trois côtés de la figure géométrique.
-
A est la zone
-
s est le demi-périmètre (trouvez le périmètre et divisez par deux) :
Dans le cas d’un triangle rectangle, l’une des jambes est la base et l’autre correspond à la hauteur. De cette façon, il est plus facile de calculer la superficie.
Propriétés et théorèmes
Théorème de Pythagore
Le théorème de Pythagore est l’un des résultats géométriques les plus célèbres et les plus utiles. Cela s'applique aux triangles rectangles, ceux qui ont un angle droit (90 degrés). Le théorème stipule que dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Mathématiquement, cela s'exprime comme suit :
a² + b² = c²
Où « a » et « b » sont les longueurs des jambes et « c » est la longueur de l'hypoténuse.
Le théorème de Pythagore est fondamental en géométrie et en trigonométrie et s'applique à une grande variété de problèmes, du calcul de distances sur des cartes à la résolution d'équations quadratiques.
Théorème de la bissectrice
Le théorème de la bissectrice fait référence à la bissectrice d'un angle dans un triangle. Il indique que la bissectrice d’un angle divise le côté opposé à l’angle en deux segments proportionnels aux deux autres côtés du triangle. Mathématiquement, cela s'exprime comme suit :
a/d = b/e
Où « a » et « b » sont les longueurs des côtés du triangle, et « d » et « e » sont les longueurs des segments en lesquels la bissectrice divise le côté opposé.
Ce théorème est utile pour calculer des segments dans des triangles et trouver des points d'intersection aux angles bissecteurs.
Théorème de Thalès
Le théorème de Thales est un outil puissant pour relier des segments dans des triangles similaires. Il stipule que si une ligne parallèle coupe deux côtés d’un triangle, elle divise ces côtés en segments proportionnels. Mathématiquement, cela s'exprime comme suit :
m/n = p/q
Où « m » et « n » sont les longueurs des segments d'un côté du triangle, et « p » et « q » sont les longueurs des segments correspondants de l'autre côté.
Le théorème de Thalès est fondamental pour résoudre des problèmes géométriques et démontrer les propriétés de triangles similaires.