La thermodynamique, branche fondamentale de la physique, dévoile les mystères du transfert de chaleur, et dans ce vaste domaine, la loi de Fourier constitue une pierre angulaire.
Ce principe, conçu par l’illustre mathématicien et physicien français Joseph Fourier au XIXe siècle, est un pilier théorique essentiel pour comprendre comment la chaleur se propage à travers les matériaux.
Cet article cherche à approfondir les nuances de cette loi, en remettant en question sa complexité inhérente avec une approche accessible et compréhensible. De ses fondements mathématiques à son application pratique dans des situations quotidiennes, nous explorerons comment la loi de Fourier apparaît non seulement dans le domaine académique mais aussi dans la vie quotidienne avec des implications importantes.
Quelle est la loi de Fourier ?
Supposons que vous ayez une tasse de café chaud dans vos mains. Vous êtes-vous déjà demandé comment la chaleur est transférée de la tasse à vos mains ? La réponse réside dans la loi de Fourier.
Cette loi stipule que le taux de transfert de chaleur à travers un matériau est proportionnel au gradient de température. Le gradient de température, en termes simples, est la différence de température entre deux points le long d'un matériau.
Ainsi, s’il y a une grande différence de température entre le café chaud et vos mains, la chaleur sera transférée plus rapidement. Plus la différence de température est grande, plus la chaleur se déplacera rapidement.
Équation de Fourier pour le transfert thermique
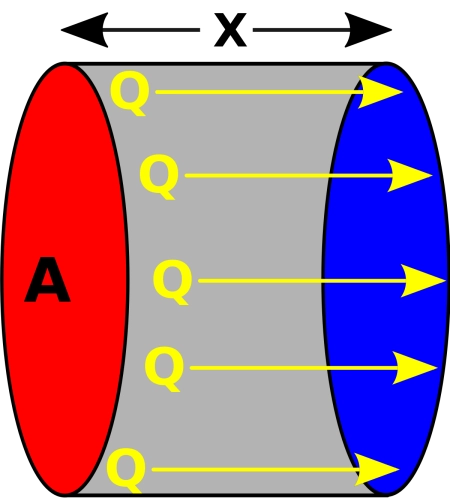
Parlons maintenant de l’équation qui représente la loi de Fourier dans un sens plus mathématique. La formule est :
\[ Q = -k A \frac{dT}{dx} \]
Où:
-
\(Q\) est le taux de transfert de chaleur (flux de chaleur).
-
\(k\) est la conductivité thermique du matériau.
-
\(A\) est la zone à travers laquelle la chaleur est transférée.
-
\(\frac{dT}{dx}\) est le gradient de température dans la direction du flux de chaleur.
Exemple réel
Appliquons maintenant la loi de Fourier à une situation quotidienne. Imaginez que vous cuisinez une délicieuse soupe dans une marmite en métal. La base de la casserole est en contact avec la cuisinière chaude et vous voulez savoir quelle quantité de chaleur est transférée à la soupe.
Tout d’abord, vous avez besoin de la conductivité thermique du métal (représentée par k ), qui est une propriété spécifique à chaque matériau. Ensuite, vous devez mesurer la surface de contact entre la base de la casserole et la cuisinière ( A ). Enfin, vous observez la différence de température entre le fond chaud de la marmite et la soupe ( dx/dT ).
En utilisant la loi de Fourier, vous pouvez calculer la quantité de chaleur transférée du poêle à la soupe.
Applications de la loi de Fourier
La loi de Fourier a diverses applications, tant en ingénierie que dans la vie quotidienne, car elle décrit le transfert de chaleur dans les matériaux. Certaines des applications les plus pertinentes incluent :
1. Conception des systèmes de chauffage et de refroidissement
 La loi de Fourier est cruciale pour la conception et l'optimisation des systèmes thermiques, tels que les systèmes de chauffage, de ventilation et de climatisation (CVC).
La loi de Fourier est cruciale pour la conception et l'optimisation des systèmes thermiques, tels que les systèmes de chauffage, de ventilation et de climatisation (CVC).
Les ingénieurs utilisent cette loi pour calculer le flux de chaleur à travers les murs, les fenêtres et les conduits d’air, contribuant ainsi à créer des environnements plus économes en énergie.
2. Isolation thermique
Dans la construction de bâtiments, la loi de Fourier est appliquée pour sélectionner des matériaux dotés de propriétés thermiques appropriées. Les matériaux isolants tels que la fibre de verre ou le polystyrène expansé sont spécifiquement conçus pour réduire le transfert de chaleur, en tirant parti des propriétés de faible conductivité thermique, ce qui contribue à maintenir des températures intérieures stables et à réduire la consommation d'énergie.
3. Ingénierie des matériaux
Dans le développement et l’étude de nouveaux matériaux, la loi de Fourier est utilisée pour prédire comment ils se comporteront sous transfert de chaleur. Ceci est important dans la fabrication de matériaux composites, de semi-conducteurs et de matériaux avancés utilisés dans l’électronique, l’aéronautique et l’énergie.
4. Électronique et appareils électroniques
Les appareils électroniques génèrent de la chaleur pendant leur fonctionnement. La loi de Fourier est utilisée pour concevoir des systèmes de dissipation thermique, tels que des dissipateurs thermiques et des ventilateurs, afin d'empêcher la surchauffe des composants électroniques.
5. Contrôle des processus thermiques
Dans des industries telles que la métallurgie, la fabrication du verre et l'industrie chimique, la loi de Fourier est essentielle pour contrôler les processus thermiques. Ces processus, tels que le refroidissement ou le chauffage des matériaux, sont conçus en tenant compte de la manière dont la chaleur est transférée au sein des matériaux.
6. Recherche sur le transfert de chaleur en biologie
En biologie, la loi de Fourier est utilisée pour comprendre comment la chaleur est transférée dans les organismes vivants, par exemple dans la régulation de la température corporelle chez les animaux à sang chaud et dans les processus métaboliques.
7. Calculs de transfert de chaleur dans le sous-sol
En énergie géothermique, la loi de Fourier est utilisée pour modéliser le transfert de chaleur à travers les couches de la Terre. Cela facilite l’exploration géothermique et la prévision de la distribution de chaleur souterraine, ce qui est important dans l’extraction de l’énergie géothermique.
8. Technologies de l'énergie solaire
La loi de Fourier est importante dans l'optimisation des panneaux solaires et du transfert de chaleur dans les systèmes solaires thermiques. Il permet de calculer comment la chaleur est distribuée et transférée au sein des systèmes de collecte d'énergie solaire.
9. Simulations thermiques en ingénierie
Les simulateurs thermiques, utilisés en génie mécanique et civil, appliquent la loi de Fourier pour modéliser la distribution de chaleur dans des structures complexes, telles que les avions, les voitures, les bâtiments ou les ponts. Ces modèles permettent de prédire les problèmes de surchauffe ou les pertes de puissance.
10. Dans l'industrie alimentaire
La loi de Fourier est appliquée dans l'ingénierie des procédés de conservation des aliments, tels que la pasteurisation ou le refroidissement des produits. Il permet de calculer la vitesse à laquelle la chaleur est transférée à travers les aliments lors de leur traitement thermique, garantissant ainsi la sécurité et la qualité du produit.
Exemple d'installation d'énergie solaire thermique
Dans le domaine de l'énergie solaire thermique, la loi de Fourier joue un rôle fondamental, car elle traite de la manière dont la chaleur est transférée à travers les matériaux, une considération essentielle dans les systèmes qui exploitent le rayonnement solaire pour générer de l'énergie thermique.
Dans cette section, nous analyserons le lien entre cette loi de la thermodynamique et une installation d'énergie solaire thermique :
Captage de l'énergie solaire
Dans une installation d’énergie solaire thermique, des capteurs solaires sont utilisés pour capter le rayonnement solaire. Ces collecteurs sont généralement composés de matériaux spécifiques aux propriétés de conduction thermique bien définies.
La loi de Fourier s'applique ici pour déterminer comment ces matériaux conduisent la chaleur de la surface du collecteur vers le fluide caloporteur en circulation.
Transfert de chaleur dans un fluide thermique
Le rayonnement solaire capté est converti en chaleur, augmentant la température du fluide thermique (tel que l’eau ou un fluide thermique spécialisé) qui circule dans les capteurs solaires.
Notre loi entre en jeu lors de l’analyse de la manière dont cette chaleur est transférée le long du fluide thermique. L'équation de loi, prenant en compte la conductivité thermique du fluide, la surface de transfert et le gradient de température, permet de comprendre et d'optimiser ce processus de transfert de chaleur.
Stockage thermique
De nombreux systèmes d’énergie solaire thermique intègrent des dispositifs de stockage thermique pour accumuler la chaleur générée pendant les périodes de rayonnement solaire maximal.
La loi de Fourier est pertinente ici pour examiner comment les matériaux de stockage thermique gèrent le transfert de chaleur pendant la charge et la décharge du système, permettant ainsi une utilisation efficace de l'énergie stockée.
Transfert de chaleur vers la charge
Enfin, dans une installation solaire thermique, la chaleur stockée est utilisée pour répondre aux besoins de chauffage ou pour produire de la vapeur qui peut entraîner des turbines et générer de l'électricité.
Dans ce processus, l’équation de Fourier est à nouveau appliquée pour examiner comment la chaleur est transférée du système de stockage à la charge, qu’il s’agisse d’un système de chauffage domestique ou d’un cycle de production d’électricité.
Qui était Joseph Fourier ?
Joseph Fourier (1768-1830) était un mathématicien et physicien français dont les contributions ont laissé une marque durable sur la science.
Né à Auxerre, il compte parmi ses réalisations le développement des séries de Fourier, un outil mathématique essentiel dans l'analyse des fonctions périodiques. Fourier a également joué un rôle crucial dans la théorie de la chaleur, en proposant la célèbre loi de Fourier, qui décrit la conduction thermique dans les matériaux.
Ses travaux l'ont conduit à devenir un membre éminent de l'Académie des sciences française et ont laissé un héritage durable dans l'étude des équations différentielles et du transfert de chaleur.