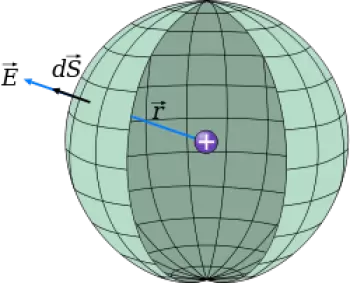
Le théorème de Gauss pour le champ électrique stipule que le flux d'un champ électrique à travers une surface fermée (surface gaussienne) est donné par le quotient entre la charge électrique totale à l'intérieur de la surface divisée par la constante diélectrique absolue du milieu (ε 0 ). Toute charge ponctuelle externe à la surface ne contribue en aucune façon au débit total.
L'équation de Gauss fait partie des quatre équations de Maxwell.
Le flux de charges qui traversent la surface gaussienne est proportionnel au nombre de lignes de champ qui la traversent.
Énoncé du théorème de Gauss
Voici l'énoncé du théorème de Gauss pour le champ électrique : le flux d'un champ électrique à travers une surface fermée est donné par la relation entre la charge électrique totale à l'intérieur de la surface et la constante diélectrique absolue du milieu.
Formule du théorème de Gauss appliqué au champ électrique
En regardant la formule du théorème de Gauss pour le champ électrique, nous pouvons écrire
La déclaration gaussienne fournit un moyen rapide et facile de calculer le flux de champ électrique à travers une surface fermée. Il s’agit simplement de calculer le champ de toutes les charges qui se trouvent à l'intérieur de la surface, les sommer et diviser la somme par la constante diélectrique absolue.
Il est important de souligner certains aspects :
-
Si l'on pense au vide, on peut substituer la constante diélectrique absolue du milieu ε m à la constante diélectrique du vide dont on connaît la valeur.
-
Pour calculer la somme algébrique de toutes les charges internes, il est nécessaire de prendre en compte les signes des charges, qui peuvent être des charges positives ou négatives.
-
La surface peut avoir n'importe quelle forme tant qu'elle est fermée.
-
Ce qui compte, c'est la charge totale à l'intérieur de la surface. S'il y a d'autres charges situées hors de la surface, elles ne doivent pas être prises en compte pour le calcul du débit.
-
Le théorème est valable pour tout type de champ électrique, pas nécessairement uniforme dans l'espace. La formule est également valable pour toute configuration de charge.