Dans le domaine de la géométrie, les plans sont des éléments basiques et fondamentaux. Définis comme des surfaces planes et infinies qui s’étendent dans toutes les directions, les plans sont des éléments fondamentaux qui nous aident à comprendre les formes et les structures en deux dimensions.
Dans cet article, nous expliquerons ce que sont les plans en géométrie, leurs caractéristiques distinctives et comment ils sont appliqués dans divers contextes mathématiques et pratiques. De la conception de figures géométriques à la résolution de problèmes et au développement d'applications technologiques, les plans jouent un rôle essentiel dans notre compréhension de l'espace et de la forme.
Qu'est-ce qu'un plan ?
En géométrie, un plan est une surface plane et infinie qui s'étend dans toutes les directions.
Vous pouvez penser à une feuille de papier qui s’étire à l’infini, sans être épaisse. Dans ce cas, il n’y a ni limites ni arêtes, c’est comme un monde infini en deux dimensions !
Caractéristiques d'un plan
Les principales caractéristiques qui définissent un plan dans l'espace sont les suivantes :
- Infini dans toutes les directions : Une des caractéristiques les plus importantes est qu’il s’étend à l’infini dans toutes les directions. Cela signifie que peu importe la distance à laquelle vous vous éloignez d’un point de le plan, vous trouverez toujours plus d’espace.
- Aucune épaisseur : Contrairement aux objets tridimensionnels, comme une balle ou un cube, un plan n’a pas d’épaisseur. Imaginez que vous regardez un dessin sur une feuille de papier. Le dessin est dans le plan du papier, mais le papier est si fin qu'on peut considérer qu'il n'a aucune épaisseur.
- Représenté par des lignes : En géométrie, nous représentons les plans à l'aide de lignes. Ces lignes peuvent être droites ou courbes et s’étendre dans toutes les directions du plan. Lorsque nous dessinons des figures géométriques sur un plan, nous utilisons ces lignes pour montrer leurs relations les unes avec les autres.
- Indépendant du système de coordonnées : Un plan est indépendant du système de coordonnées utilisé pour le représenter. Cela signifie que quelle que soit la manière dont les axes x et y sont choisis, les propriétés fondamentales du plan, telles que son infinité et son manque d'épaisseur, restent inchangées.
- Contient une infinité de points : Puisqu’il s’étend à l’infini, il contient une infinité de points. Chaque point du plan est unique et peut être identifié par ses coordonnées, si un système de coordonnées est utilisé.
- Il ne détermine pas de direction préférentielle : contrairement aux lignes et segments, qui ont une direction spécifique, le plan lui-même n'a pas de direction préférentielle. Elle peut être considérée comme une surface sans orientation dans laquelle les directions sont également valables.
Types de plans
En géométrie, il existe plusieurs types des plans utilisés à des fins et applications différentes. Voici quelques-uns des types les plus courants :
- Horizontal : Un plan horizontal est un plan qui s'étend horizontalement par rapport à la surface de la Terre. Dans un système de coordonnées tridimensionnelles, un plan horizontal ne s'incline ni ne dévie verticalement.
- Vertical : Contrairement au précédent, un plan vertical s'étend verticalement et est perpendiculaire à la surface terrestre. Le vertical est utile en géométrie pour représenter les relations spatiales dans un espace tridimensionnel.
- Incliné : Un plan incliné est un plan qui n'est ni horizontal ni vertical, mais qui forme un angle par rapport aux deux. Les inclinés sont courantes dans les problèmes de physique et de mécanique, où elles sont utilisées pour étudier les forces, les pentes et le mouvement.
- Cartésien : ce type est un système de coordonnées bidimensionnel composé de deux axes perpendiculaires, généralement appelés x et y. Il est largement utilisé en mathématiques pour représenter des points, des graphiques et des fonctions.
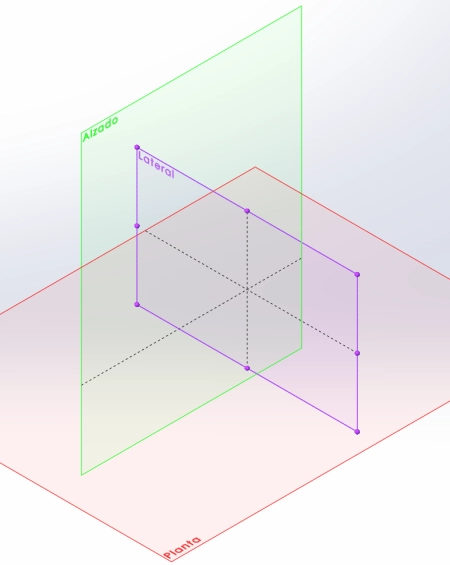
- Projection : Dans le dessin technique et la conception, un plan de projection est utilisé pour représenter des objets tridimensionnels en deux dimensions. Les plans de projection comprennent trois plans : plan, élévation et côté, qui montrent différentes vues de l'objet sous différents angles.
- Tangente : un plan tangent est un plan qui touche une surface en un seul point et est perpendiculaire à la ligne qui passe par ce point. Les plans tangents sont importants dans le calcul et la géométrie différentielle pour représenter la relation entre les courbes et les surfaces en un point donné.
- Parallèle : Un plan parallèle est un plan qui ne coupe pas un autre plan donné et qui maintient la même distance sur toute sa longueur. Les plans parallèles sont utiles en géométrie pour étudier les propriétés des lignes et des angles par rapport aux surfaces parallèles.
- Perpendiculaire : Un plan perpendiculaire est un type spécial qui forme un angle droit (90 degrés) par rapport à un autre plan ou à une ligne.
Différence entre plan et aire
En géométrie, le terme "plan" fait référence à une surface bidimensionnelle s'étendant à l'infini dans toutes les directions, semblable à une feuille de papier. C'est une entité abstraite sans épaisseur, définie par l'intersection de deux lignes ou par des séquences de points dans l'espace.
D'autre part, "aire" est une mesure quantitative de l'étendue d'une surface bidimensionnelle. Elle représente la quantité d'espace couverte par une figure dans le plan et s'exprime en unités carrées (comme des mètres carrés ou des centimètres carrés).
Tandis qu'un plan est la surface en elle-même, l'aire est la mesure numérique de l'espace occupé par cette surface.