La géométrie, l'une des branches fondamentales des mathématiques, est responsable de l'étude des formes, des tailles, des positions relatives des objets géométriques et des propriétés de l'espace. Au sein de cette discipline, l'un des concepts clés est la bissectrice.
En termes simples, une bissectrice est une ligne, un rayon ou un segment qui divise quelque chose en deux parties égales ou proportionnelles.
Le terme « bissectrice » vient du latin « bisectus », qui signifie « couper en deux ». La bissectrice est utilisée dans différents contextes géométriques pour diviser les angles, segments, arcs et autres éléments en parties égales ou proportionnelles.
Nous explorerons ensuite comment la bissectrice est appliquée dans diverses situations géométriques.
Bissectrice d'un angle
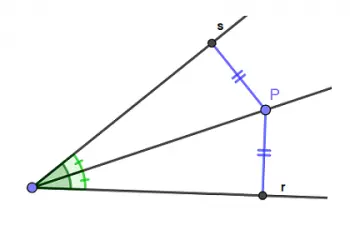
L'une des applications les plus courantes de la bissectrice en géométrie est la division des angles. La bissectrice d'un angle est une ligne qui divise cet angle en deux angles plus petits ayant la même mesure.
En d’autres termes, divisez l’angle en deux parties égales. Ceci est utile pour couper des angles, construire des angles spécifiques et résoudre des problèmes géométriques.
La bissectrice d'un angle peut être visualisée comme une ligne qui part du sommet de l'angle et le divise en deux angles congrus.
Bissectrice d'un segment
La bissectrice peut également être appliquée aux segments de droite. La bissectrice d'un segment divise le segment en deux parties de même longueur. Si nous avons un segment AB, la bissectrice le divisera en deux segments AC et CB, où AC est de longueur égale à CB.
Cette propriété est particulièrement utile pour trouver le milieu d'un segment, ce qui a des implications significatives en géométrie analytique et dans la construction de figures géométriques équidistantes.
Bissectrice d'un arc
En géométrie circulaire, une bissectrice d’arc est une ligne qui coupe l’arc exactement en deux. Ceci est très utile dans les problèmes de géométrie où une division précise d'un cercle ou d'un arc est requise.
La bissectrice d'un arc sert par exemple à déterminer le centre d'un cercle ou à diviser un cercle en deux arcs de même longueur. Ceci est essentiel dans la construction de figures géométriques circulaires et dans la résolution de problèmes liés aux cercles.
Bissectrice en triangles
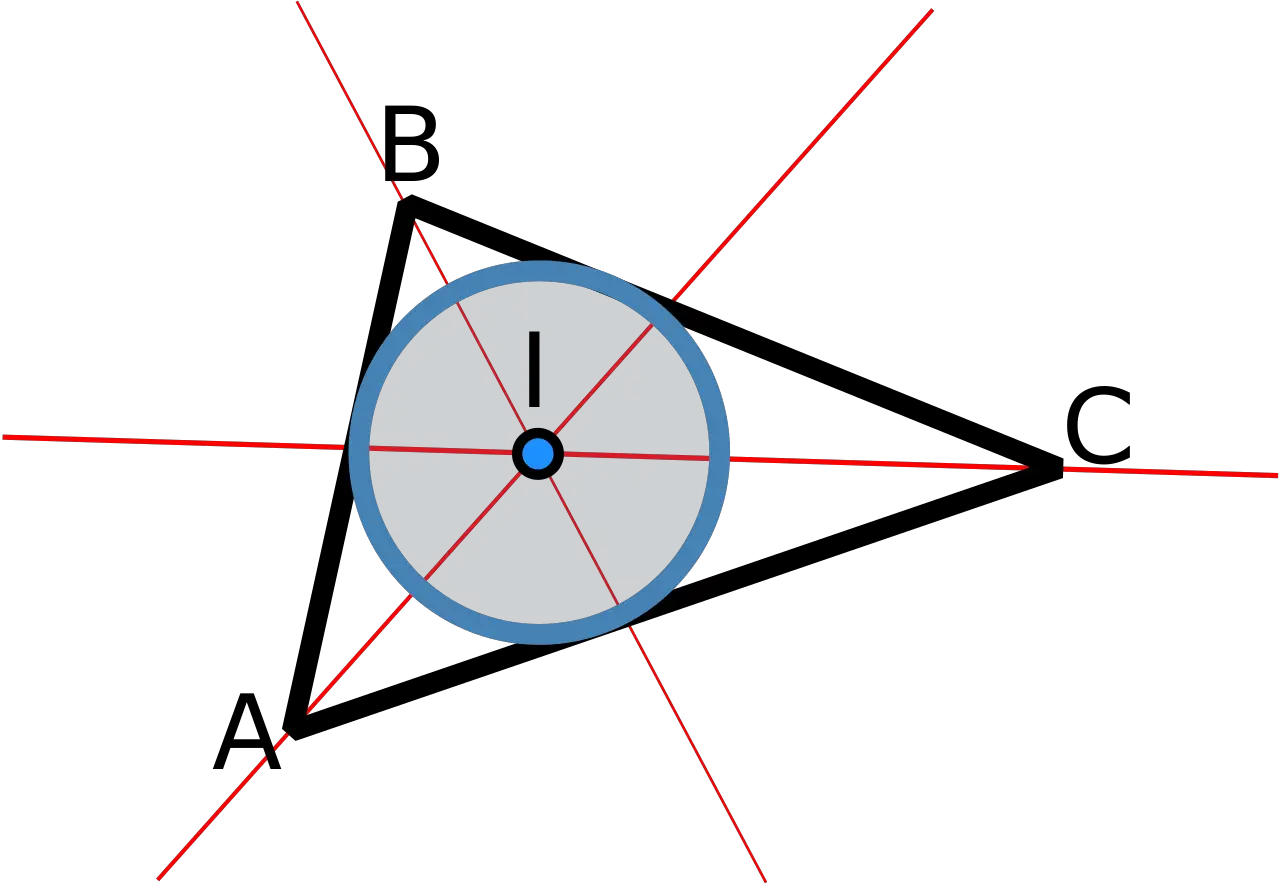Cet élément joue également un rôle important dans l’étude des triangles.
Dans un triangle, la bissectrice d'un angle est une ligne qui part du sommet de l'angle et divise le côté opposé en deux segments proportionnels aux deux autres côtés du triangle. Ceci est connu sous le nom de « théorème de la bissectrice » et est utile pour résoudre des problèmes de trigonométrie et prouver les propriétés des triangles.
Le théorème stipule que le rapport entre la longueur d’un côté du triangle et la longueur du segment que forme la bissectrice de ce côté est égal au rapport entre les deux autres côtés du triangle.
Cette propriété est d’une grande importance dans la résolution de problèmes géométriques impliquant des triangles et leurs caractéristiques.
Applications de la bissectrice dans la vie quotidienne
Par exemple, en architecture, il est utilisé pour construire des angles précis et des divisions proportionnelles dans les plans et les conceptions des bâtiments. La bissectrice permet aux architectes et aux concepteurs de créer facilement des structures symétriques et équilibrées.
En ingénierie, la bissectrice est utilisée pour déterminer des points équidistants sur les structures et les machines, ce qui est essentiel pour garantir la stabilité et la précision dans diverses applications.
Conclusion
La bissectrice est un concept fondamental en géométrie utilisé pour diviser les angles, segments, arcs et autres éléments en parties égales ou proportionnelles.
Son application est large et polyvalente, jouant un rôle essentiel dans la résolution de problèmes géométriques, la construction de figures géométriques et la démonstration de propriétés mathématiques. Comprendre la bissectrice est essentiel pour ceux qui souhaitent entrer dans le monde de la géométrie et de ses applications dans diverses disciplines.
De la division précise des angles en architecture à la résolution de problèmes de trigonométrie en mathématiques, la bissectrice est un outil puissant qui joue un rôle de premier plan dans la résolution de problèmes et la création de structures équilibrées et symétriques.
