Un cercle est une forme géométrique plane dont les points sont à égale distance d'un point donné sur un plan euclidien (le centre du cercle). La distance des points situés sur le périmètre de cette forme au centre est le rayon. Le mot cercle est dérivé d'un mot grec qui signifie « cerceau ou anneau ».
Ne confondez jamais un cercle avec un polygone. Ce n'est pas un polygone car il est composé de courbes.
L'histoire de cette forme est ancienne. Les gens croyaient que la lune, le soleil et les autres planètes étaient circulaires parce qu'il n'y avait pas de concept de formes tridimensionnelles ; les mathématiciens ont étudié des cercles qui les ont aidés à développer le calcul et l'astronomie.
Les cercles congruents ont le même rayon, quel que soit l'endroit où se trouvent leurs centres.
Quelle est la différence entre un cercle et une circonférence ?
Un cercle est une surface plane délimitée par une série de points en forme de courbe.
De l'autre côté, une circonférence est une ligne courbe continue. Par conséquent, une circonférence est le périmètre d'un cercle, c’est à dire, le bord du cercle. Puisque la circonférence est une ligne et non une surface plane, elle n'a pas d'aire, mais elle a un périmètre.
La différence entre les deux est que le cercle est la zone entière contenue dans la circonférence, tandis que la circonférence est le bord extérieur du cercle.
Quelles sont les parties d’un cercle ?
Il y a plusieurs points, lignes et segments singuliers sur la circonférence :
-
Centre : c'est le point fixe intérieur équidistant de tous les points de la circonférence.
-
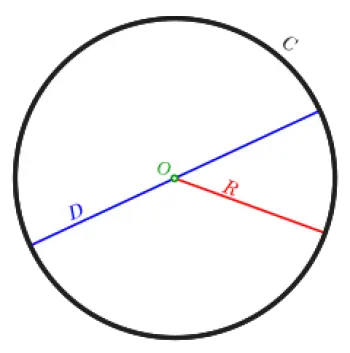
Diamètre : c'est la droite qui joint deux points opposés de la circonférence en passant par son centre.
-
Rayon : segment qui rejoint le centre avec un point sur le périmètre. La longueur du rayon c’est la moitié de la longueur du diamètre.
-
Corde : la corde d'un cercle s'obtient en traçant une droite joignant deux points sur la circonférence. L'accord divise la forme en segment mineur - qui a la plus petite surface - et en segment majeur.
-
Ligne sécante : celle qui coupe la circonférence en deux points.
-
Ligne tangente : la ligne qui touche la circonférence en un seul point.
-
Point tangent : le point de contact de la tangente avec la circonférence.
-
Arc d’un cercle: C'est un segment du cercle. Ainsi, tous les points appartiennent à sa circonférence.
-
Demi-cercle : est un secteur circulaire équivalent à la moitié du périmètre. Les extrémités d'un diamètre délimitent un demi-cercle.
Comment calculer l'aire d'un cercle ?
La formule pour calculer l'aire du disque est :
A = π · r 2
où,
-
π est le nombre Pi , une constante mathématique qui vaut environ 3,1416.
-
"r" est le rayon dont l'unité dans le système de mesure international est le mètre (m), bien que d'autres mesures de longueur puissent être utilisées.
-
"A" est la surface totale. Si la formule a été calculée avec le rayon exprimé en mètres, les unités de la surface seront les mètres carrés (m²).
Comment calculer le périmètre d’un cercle ?
La formule de la circonférence est :
P = 2 · π · r
où
-
P est le périmètre.
-
π est la constante Pi qui vaut 3,146.
-
r est le rayon du cercle.
Calcul du diamètre d’un cercle
On peut définir le diamètre du cercle à l'aide de la formule pour trouver le périmètre ou l'aire selon que l'on connaît la valeur du périmètre ou de l'aire.
Pour ce faire, il suffit de considérer que le diamètre (d) est le double de la valeur du rayon (r). Par conséquent, nous pouvons substituer (r) à (d/2) dans les formules ci-dessus.
Les deux formules pour trouver le diamètre sont :
-
Si nous connaissons l'aire (A) : d = 2 √(A/π), la racine carrée de l'aire divisée par pi et multipliée par 2.
-
Si on connaît le périmètre (P) : d = P / π
-
Si nous connaissons le rayon (r) de la circonférence : d = 2 · r