
Un carré est une forme géométrique régulière avec quatre côtés égaux et quatre angles droits (90 degrés) entre ces côtés. C’est à dire, les côtés consécutifs d’un carré sont perpendiculaires.
Un carré peut être classé comme un polygone régulier, un quadrilatère plan fermé et un quadrilatère convexe. Cette figure plane est un cas particulier du rectangle, du losange, du parallélogramme, du trapèze et du cerf-volant.
Pour reconstruire cette forme, il suffit de connaître la longueur du côté ou de la diagonale.
Les carrés apparaissent dans de nombreux solides géométriques, mais un cas particulier est un cube. Un cube est un solide platonique dont toutes ses faces (six) sont constituées de carrés. Le cube est le seul solide platonicien à faces carrées.
Le carré est aussi la forme de base d'une mosaïque platonicienne.
Les propriétés d'un carré
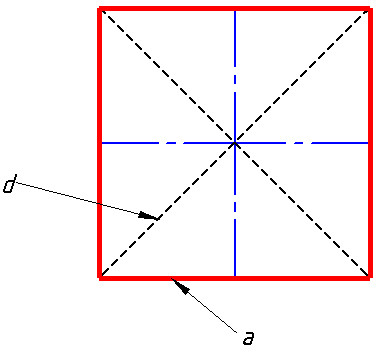
-
Les quatre côtés ont la même longueur. C'est donc un losange et un polygone équilatéral.
-
Les quatre angles intérieurs sont égaux, c'est donc un rectangle et un polygone équiangulaire. Par conséquent, les angles intérieurs sont des angles droits (mesurez 90º).
-
Totes les côtés opposées d’un carré sont parallèles.
-
Les deux diagonales du carré sont égales, se coupent en leur milieu et sont orthogonales.
-
La limite d'un carré est quatre fois la longueur d'une arête.
-
Le point d'intersection des diagonales est le centre du carré, le centre circonscrit, le cercle inscrit et le centre de symétrie. Le carré est à la fois une corde et une tangente quadrilatérale.
-
L'aire du cercle circonscrit est le double de l'aire du cercle de centre inscrit.
-
Il a quatre axes de symétrie : les deux bissectrices perpendiculaires et les diagonales.
-
Il est quadruple à symétrie de rotation et donc également à symétrie ponctuelle.
-
Le groupe de symétrie est le groupe dièdre D4.
En géométrie euclidienne, le carré est le cas bidimensionnel particulier de l'hypercube et du polytope croisé.
La notion de carré est généralisée en géométrie synthétique plane affine en utilisant l'un des énoncés équivalents décrivant un carré en géométrie élémentaire pour définir l'idée. Par exemple, pour les plans pré-euclidiens, l'existence de ces figures devient une hypothèse supplémentaire.
Dans les géométries non euclidiennes, les carrés sont généralement des polygones avec quatre côtés égaux et des angles intérieurs égaux.
Un carré est un polygone de géométrie sphérique dont les côtés sont de grands cercles se coupant au même angle. Contrairement aux carrés de géométrie plane, les angles d'un carré sphérique sont plus significatifs qu'un angle droit. Par conséquent, les carrés sphériques plus grands ont des angles plus grands.
Les carrés à angle droit n'existent pas en géométrie hyperbolique. Au lieu de cela, les carrés ont des angles inférieurs à un angle droit. Les grands carrés hyperboliques ont des angles plus petits.
Théorème de Pythagore
Pour trouver la longueur du côté, on peut utiliser le théorème de Pythagore.
Il faut savoir que d'après le théorème de Pythagore :
-
L'hypoténuse d'un triangle rectangle est égale à la racine carrée de la somme des carrés des jambes.
-
La jambe d'un triangle rectangle est égale à la racine carrée de l'hypoténuse au carré moins l'autre jambe au carré.
Selon sa formule :
d2 = a2 + a2
Donc, a = √(d2 / 2)
Formule pour calculer l'aire d'un carré
Pour trouver l'aire, on peut utiliser la formule suivante :
où
-
A est la forme de la surface totale.
-
a est la longueur d'un côté (ils sont tous identiques)
-
d est la longueur de la diagonale du carré d'un sommet au sommet opposé.
Périmètre d'un carré
Le carré du périmètre est la longueur totale de ses côtés, la longueur de la frontière. Voici la formule pour trouver le périmètre de la forme :
P = 4 · a
où,
-
P est le périmètre de la figure géométrique
-
a est la longueur d'un côté du carré.
Autres figures géométriques qui peuvent être un carré
Le carré peut également être défini dans d'autres figures géométriques si elles remplissent certaines conditions :
-
Un rectangle avec deux côtés adjacents de même longueur.
-
Un losange avec deux angles égaux adjacents.
-
Un losange avec un angle droit.
-
Un parallélogramme avec deux côtés adjacents égaux et deux angles adjacents égaux.
-
Un parallélogramme avec deux côtés adjacents égaux et un angle droit.
-
Un quadrilatère dont les diagonales orthogonales de même longueur se coupent en leur milieu.
