La géométrie est une branche des mathématiques qui se concentre sur l'étude des formes, des tailles et des propriétés des objets géométriques, tels que les points, les lignes, les segments, les polygones et les cercles.
L'un des sujets fondamentaux de la géométrie, et en particulier des triangles, est l'étude des angles et des segments, et l'un des théorèmes les plus importants liés à ces concepts est le théorème de la bissectrice.
Ce théorème joue un rôle crucial dans la division des angles et des segments et a des applications dans divers domaines des mathématiques et de la physique.
Définition des angles et de la bissectrice
Avant de plonger dans le théorème de la bissectrice, il est important de comprendre certains concepts clés de la géométrie. Un angle est la région formée par deux rayons partageant un point commun, appelé sommet. Les angles sont mesurés en degrés et un angle complet est de 360 degrés. Dans de nombreux cas, il faut diviser un angle en deux parties égales, ce qui nous amène à la notion de bissectrice.
Une bissectrice d'angle est une ligne, un rayon ou un segment qui divise l'angle en deux angles congrus, c'est-à-dire deux angles qui ont la même mesure. En d’autres termes, la bissectrice coupe l’angle de moitié. Dans le cas d’un angle de 90 degrés, la bissectrice résultante aurait un angle de 45 degrés de chaque côté.
Le théorème de la bissectrice du triangle
Le théorème de la bissectrice stipule que, dans un triangle, la bissectrice d'un angle divise le côté opposé en segments proportionnels aux deux autres côtés. Cela peut sembler une déclaration complexe, mais nous pouvons la décomposer et mieux la comprendre à travers un exemple.
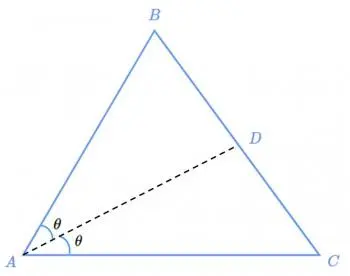
Considérons un triangle ABC, où l'angle au sommet A est divisé en deux par une ligne traversant le côté opposé BC au point D. Le théorème nous dit que le rapport entre BD et CD est égal au rapport entre AB et AC.
Mathématiquement, cela peut s'exprimer ainsi :
Ce théorème est particulièrement utile pour résoudre des problèmes de géométrie impliquant des angles et des segments. Cela peut nous aider à trouver des longueurs inconnues ou à démontrer les propriétés des triangles et d’autres figures géométriques.
Preuve du théorème de la bissectrice
La preuve du théorème de la bissectrice implique l'utilisation des propriétés de triangles similaires et l'application du théorème de Thales. Voici une brève explication de la façon dont cela est démontré :
-
On commence par le triangle ABC et sa bissectrice qui coupe le côté BC au point D.
-
Nous appliquons le théorème de Thales, qui stipule que si nous avons deux droites parallèles coupées par des droites transversales, des segments proportionnels sont créés. Dans ce cas, on trace une ligne parallèle aux côtés AC et BD qui passe par le point C.
-
Cela nous donne deux triangles similaires : ACD et ABC, où les angles sont égaux et les droites parallèles, ce qui implique des segments proportionnels.
-
En utilisant la propriété de similarité des triangles, nous pouvons affirmer que :
C’est l’égalité que nous voulions prouver, et ainsi la preuve du théorème est terminée.
Exemples d'applications du théorème
Le théorème de la bissectrice a plusieurs applications en géométrie et en mathématiques. Certains des exemples d'applications les plus courants incluent :
- Résolution de problèmes de géométrie : le théorème est utilisé pour trouver des longueurs ou des angles inconnus dans des triangles et d'autres figures géométriques lorsque certaines relations de proportion sont connues.
- Démonstration des propriétés des triangles : Utilisé pour montrer que certains triangles sont similaires ou que certains points sont sur une droite.
- Construction géométrique : aide à construire des angles coupés en deux avec précision, ce qui est utile dans diverses applications de conception et d'architecture.
- Études de trigonométrie : Le théorème est également appliqué en trigonométrie pour résoudre des problèmes liés aux sinus, cosinus et tangentes.
- Résolution de problèmes de physique : utilisé en physique pour comprendre les trajectoires des particules et la direction des forces dans les systèmes physiques.
