
L'entropie en physique et en chimie est la grandeur qui indique l'énergie qui ne peut pas effectuer de travail pratique dans un processus thermodynamique. En général, l'entropie totale de l'univers tend à augmenter. Par conséquent, l'entropie, c'est-à-dire l'augmentation de l'entropie, donc la variation positive de cette grandeur indique le sens naturel dans lequel un événement se produit dans un système isolé.
L'entropie est une grandeur thermodynamique initialement définie comme un critère pour prédire l'évolution des systèmes thermodynamiques. Dans tout processus irréversible, le désordre du système augmente, et donc l'entropie augmente. Dans les processus réversibles, le bilan entropique est nul.
L'entropie d'un système est une fonction d'état extensive. La valeur de cette grandeur physique, dans un système fermé (sans changement d’énergie au milieu extérieur), est la mesure du désordre qu'un processus génère naturellement. Le concept d'entropie décrit à quel point un système thermodynamique est une transformation irréversible.
En la thermodynamique classique il n’est pas possible de calculer l’entropie absolue d’un système. Par conséquent, les scientifiques étudient la variation d’entropie du système.
Dans le processus non réversible, une partie de l'énergie se transforme en entropie en raison de la conservation de l'énergie.
Quelle est l'unité d'entropie ?
Les unités d'entropie dans le système international sont les joules/kelvin (J/K) ou Clausius.
Nous définissons cette unité SI comme le changement d'entropie subi par un système lorsqu'il absorbe l'énergie thermique de 1 Joule (unité) à une température de 1 Kelvin.
Formule d'entropie en physique
En physique, l'entropie du système est la grandeur thermodynamique qui permet de calculer la part d'énergie thermique qui ne peut pas être utilisée pour produire du travail si le processus est réversible. L'entropie physique, sous sa forme classique, est définie par l'équation proposée par Rudolf Clausius :
![]()
Où dS est la variation de l'entropie, dQ est la variation d'énergie et T est la température. ou plus simplement, si la température est maintenue constante dans le processus (processus isotherme).
Ainsi, si un corps chaud à la température T1 perd une quantité de chaleur Q1, son entropie diminue en Q1/T1. S'il transfère cette chaleur à un corps froid à température T2 (inférieure à T1), l'entropie du corps froid augmente plus que l'entropie du corps chaud ne diminue car
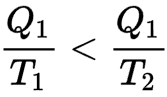
Un moteur réversible peut donc transformer une partie de cette énergie calorifique en travail.
Pourquoi n'est-il pas possible de connaître l'entropie absolue ?
Il est impossible de déterminer l'entropie absolue dans le monde réel car cela nécessiterait d'atteindre la température de zéro kelvin.
En physique, on travaille toujours sur la variation d'entropie car pour connaître la valeur absolue, il faudrait d'abord atteindre le zéro absolu. Pour arriver au zéro absolu, il faudrait que le système se refroidisse à zéro kelvin pour que les molécules ne bougent plus. À partir de là, augmenter la température augmenterait l'entropie.
Cependant, d'un point de vue physique, il est impossible d'atteindre la température de zéro kelvin, selon le théorème de Walther Nernst présenté dans le troisième principe de la thermodynamique.
Qu'est-ce que l'entropie standard ?
L'entropie standard d'un composé chimique est son entropie sous l'état thermodynamique de 1 atm de pression. Ces valeurs sont exprimées dans une table d'entropie généralement indiquée à une température de 298 K.
Habituellement, dans ces tableaux, les enthalpies de formation des éléments chimiques dans leurs états standards fixés à zéro sont également exprimées. L'enthalpie de formation est la quantité d'énergie nécessaire pour former ces compositions.
Performances d'un moteur thermique réversible
La performance de la machine réversible indique le rapport maximum d'énergie qui peut fournir du travail. La formule suivante peut exprimer cette relation :
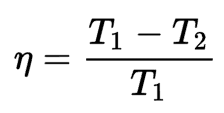
Pour que toute l'énergie calorifique soit transformée en travail, il faudrait soit que le point chaud soit à une température infinie, soit que le point froid soit à zéro kelvin ; sinon, le rendement thermodynamique du moteur réversible est inférieur à 1.
Quelle relation existe-t-il entre l'entropie et l'énergie?
En supposant que l'univers entier est un système isolé, c'est-à-dire un système pour lequel il est impossible d'échanger matière et énergie avec l'extérieur, le premier principe de la thermodynamique et le second principe de la thermodynamique peuvent être résumées comme suit: " l'énergie totale de l'univers est constante et l'entropie totale augmente continuellement jusqu'à ce qu'elle atteigne l'équilibre ».
Cela signifie que non seulement il ne peut pas créer ou détruire l'énergie, ni se transformer complètement d'une forme à une autre sans qu'une partie ne se dissipe sous forme de la chaleur.
Comment et qui a découvert le concept d'entropie?
 Le concept d'entropie est développé en réponse à l'observation d'un certain fait: il y a une certaine quantité d'énergie libérée dans les réactions de combustion qui est perdue à cause de la dissipation ou du frottement. De cette façon, l'énergie perdue n'est pas transformée en travail utile.
Le concept d'entropie est développé en réponse à l'observation d'un certain fait: il y a une certaine quantité d'énergie libérée dans les réactions de combustion qui est perdue à cause de la dissipation ou du frottement. De cette façon, l'énergie perdue n'est pas transformée en travail utile.
Recherches sur les premiers moteurs thermiques
Les premiers moteurs thermiques tels que le Thomas Savery (1698), le moteur Newcomen (1712) et le Cugnot à vapeur à trois roues (1769) étaient inefficaces. De l'énergie d'entrée, seulement 2% ont été convertis en énergie utile.
Une grande quantité d'énergie utile a été dissipée ou gaspillée dans ce qui semblait être un état aléatoire incommensurable.
Au cours des deux siècles suivants, les physiciens ont étudié ce casse-tête d'énergie perdue.
Le résultat de ces études a conduit les scientifiques au concept d'entropie.
Premières occurrences du concept d'entropie
L’entropie d’un système a été introduite en 1865 par Rudolf Clausius dans la thermodynamique classique.
Depuis lors, diverses définitions de l'entropie sont apparues. La définition la plus pertinente de l'entropie est celle développée par Ludwig Boltzmann. Boltzmann relie le concept d'entropie au degré de désordre d'un système. Cette nouvelle perspective d'entropie a permis d'étendre le concept à différents domaines, tels que la théorie de l'information, l'intelligence artificielle, la vie ou le temps.