En géométrie, les corps géométriques constituent une catégorie essentielle de formes tridimensionnelles qui occupent l'espace en trois dimensions : hauteur, largeur et longueur. Ces solides, définis par des faces, des arêtes et des sommets, jouent un rôle fondamental dans la conceptualisation et la compréhension des structures tridimensionnelles.
L'importance de ces figures géométriques tridimensionnelles réside dans leur capacité à décrire des objets réels et abstraits dans l'espace, ce qui est crucial dans des domaines tels que l'architecture, le design et l'ingénierie.
Un exemple classique est le cube, avec ses six faces carrées et ses sommets connectés, qui représente un solide géométrique élémentaire. La diversité des corps géométriques, des pyramides aux cylindres, permet de modéliser et de comprendre la richesse des formes que l'on retrouve dans le monde tridimensionnel qui nous entoure.
Qu'est-ce qu'un corps géométrique ?
Un corps géométrique est une entité tridimensionnelle qui occupe l'espace dans les dimensions de hauteur, de largeur et de profondeur. Se différenciant des figures bidimensionnelles, ces solides tridimensionnels possèdent des faces, des arêtes et des sommets qui définissent leur structure. Les corps géométriques englobent diverses formes, des prismes et pyramides aux sphères et cylindres, chacun ayant des propriétés uniques.
Les faces plates, les arêtes vives et les sommets connectés contribuent à la caractérisation de ces solides dans l'espace tridimensionnel.
En plus de leur importance en géométrie et en mathématiques, les corps géométriques sont utilisés dans des applications pratiques en architecture, en design et en sciences, servant d'outils essentiels pour conceptualiser et modéliser des objets dans le monde tridimensionnel.
Polyèdres : un cas particulier
Les polyèdres sont un cas particulier de corps géométriques dont les faces sont toutes des polygones. Parmi eux, on peut distinguer les polyèdres réguliers et les polyèdres irréguliers.
En géométrie tridimensionnelle, un polyèdre est l'équivalent de n'importe quel polygone en géométrie bidimensionnelle.
Les polyèdres réguliers sont constitués de polygones réguliers. Ces corps géométriques peuvent être classés selon le nombre de faces.
Les polyèdres réguliers sont les plus symétriques. Il existe au total neuf polyèdres réguliers : cinq polyèdres convexes et quatre polyèdres étoilés .
Un polyèdre convexe est un polyèdre qui matérialise un solide convexe, c'est-à-dire que pour chaque paire de points du solide, le segment linéaire qui les joint est entièrement contenu dans le solide.
Les cinq exemples convexes sont connus depuis l'Antiquité et sont appelés polyèdres platoniciens. Ce sont la pyramide triangulaire ou tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre.
Tronc pyramidal
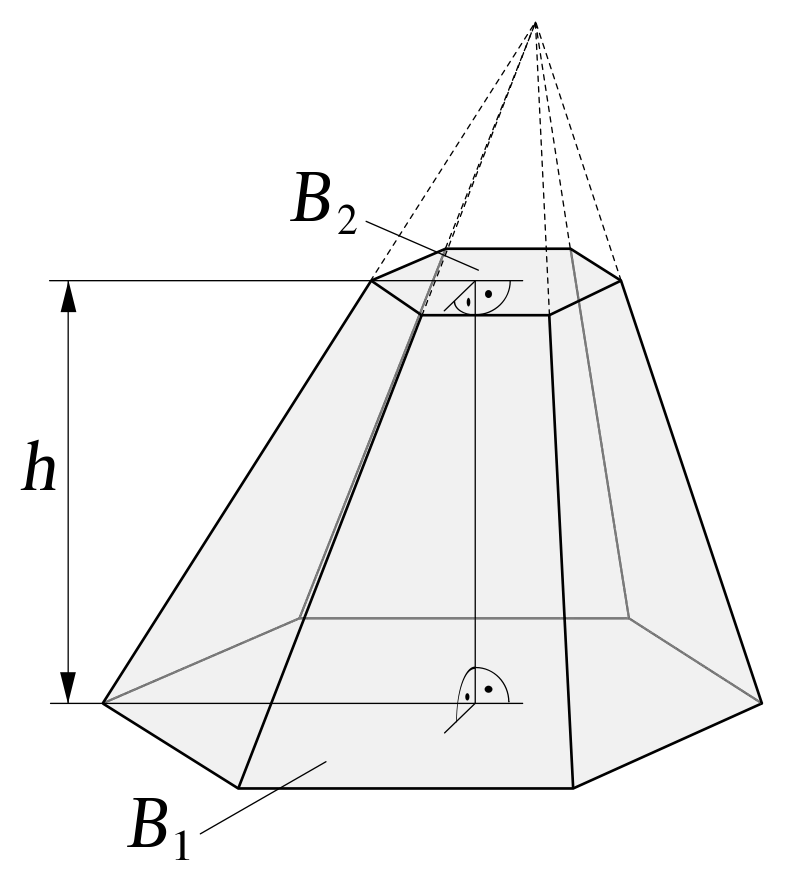Le tronc de pyramide est un type de polyèdre composé de deux bases parallèles avec le même nombre d'arêtes. En revanche, il est composé de faces latérales en forme de trapèze. Le nombre de faces est le même que le nombre d'arêtes des bases.
Ce polyèdre est obtenu en sectionnant une pyramide avec un plan intermédiaire parallèle à sa base. Des deux pièces résultantes, la partie inférieure est une pyramide tronquée et la partie supérieure reste une pyramide.
Prismes
Un prisme est un polyèdre dont deux de ses faces sont égales et se trouvent dans des plans parallèles. Les faces restantes du prisme sont des parallélogrammes qui ont des côtés communs avec ces polygones. Ces parallélogrammes sont appelés faces latérales du prisme, et les deux polygones restants sont appelés bases.
Le polygone trouvé à la base détermine le nom du prisme, par exemple : si les bases sont des triangles c'est un prisme triangulaire.
Selon la base, le prisme peut être nommé comme suit :
- Prisme triangulaire : chaque base a la forme d'un triangle.
- Prisme quadrangulaire : chacune des bases a la forme d'un quadrilatère.
- Prisme pentagonal : chacune des bases a la forme d'un pentagone.
- Prisme hexagonal : chaque base a la forme d'un hexagone.
- Prisme octogonal : chaque base a la forme d'un octogone.
Corps ronds
Nous définissons les corps ronds comme des corps géométriques possédant au moins une face incurvée. Ce type de corps est également appelé corps de révolution car ils peuvent être obtenus en faisant tourner une figure géométrique autour d'un axe.
Voici quelques exemples de corps ronds :
- La sphère est la figure générée par la rotation d'un cercle passant par un axe qui passe par le centre. Dans ce cas, il présente une seule surface courbe et aucun bord. De plus, tous les points de la surface sont équidistants du centre de la sphère.
- Le cône est généré en faisant tourner un triangle rectangle autour d'une de ses pattes. Cette figurine présente une seule face plane formée par un cercle.
- Le cylindre est formé en faisant tourner un rectangle autour d'un de ses côtés.
Exemples quotidiens
- Ballon de football : Affichant la perfection d'une sphère, le ballon de football illustre la présence courante de cette forme géométrique dans les objets du quotidien.
- Planètes du système solaire : Les corps célestes du système solaire adoptent des formes sphériques, soulignant la prédominance de la sphère dans la configuration de l'univers.
- Boîte en carton : Avec sa structure qui épouse la forme d'un prisme rectangulaire, appelé cuboïde, les boîtes en carton sont des exemples tangibles de figures géométriques dans les emballages courants.
- Pyramides d'Egypte : Représentant la majesté architecturale, les pyramides sont des exemples de pyramides quadrangulaires qui ont résisté à l'épreuve du temps.
Ces exemples illustrent à quel point la géométrie est intrinsèquement présente dans notre environnement, des objets du quotidien aux monuments historiques.
